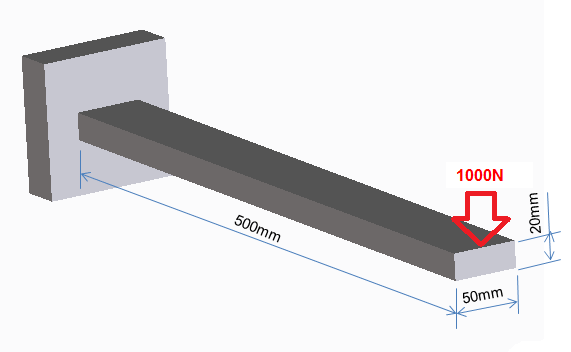
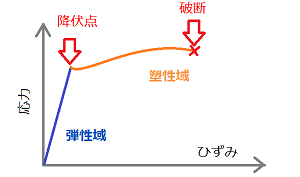
特異点付近の応力分布を見てみよう
左端を固定端(X、Y、Z軸に対して固定)、右端に1,000Nの荷重条件を設定しています。たわみは10倍に拡大して、片持ち梁の変位を目視で確認できるようにしています。
CAE結果と理論値との差異
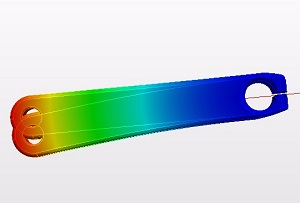
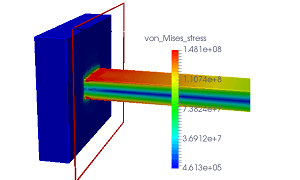
理論値は150MPaですが、CAEによって求めたミーゼス応力の最大値は152.3MPa、主応力の最大値は213.2MPaとなっています。固定端である左端に最大応力が出るはずですが、ミーゼス応力の最大値は少し右側に寄っています。
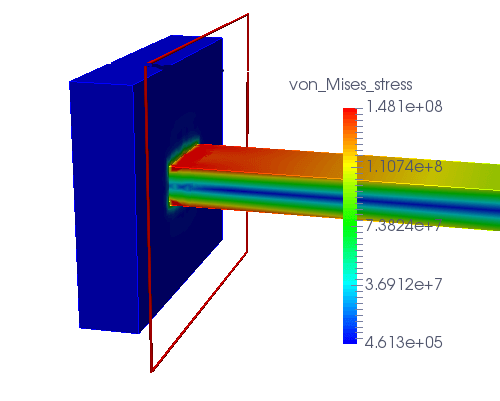
ミーゼス応力(152.3MPa)
主応力(213.2MPa)

特異点が出現した原因は?
金属原子は、結晶の中で僅かに動くことができます。ところが、左端の面を固定したことにより、金属原子が動けなくなってしまい、実際には原子がずれることで集中しない応力が発生してしまうのです。そのため、特異点近傍の応力は理論値より高くなります。
拘束面の近傍以外にも、フィレットや鋭角な角度変化がある箇所では、4面体や6面体で構成されるメッシュに角度がついてしまうために、特異点が出現しやすくなります。
特異点による応力集中箇所を避けて評価する
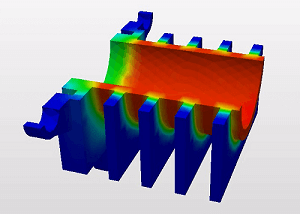
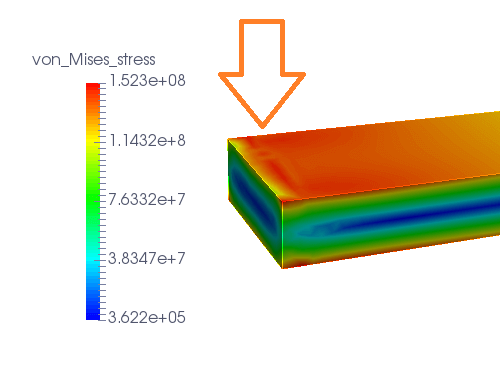
特異点によって応力が高く算出されることがわかっていれば、応力集中箇所を避けて応力を測定することで過剰評価を防げます。下図の解析結果では応力の強弱を色分けして表示していますが、赤色で表示されている箇所が応力集中箇所です。
解析モデルの最大応力を測定すると当然この赤色箇所が含まれてしまいます。そこで、応力集中箇所の右側に測定ポイント(赤枠内)をずらして、応力を測定します。
片持ち梁の固定端近傍の応力集中

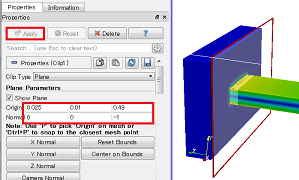
応力集中箇所を避けて測定面を設置
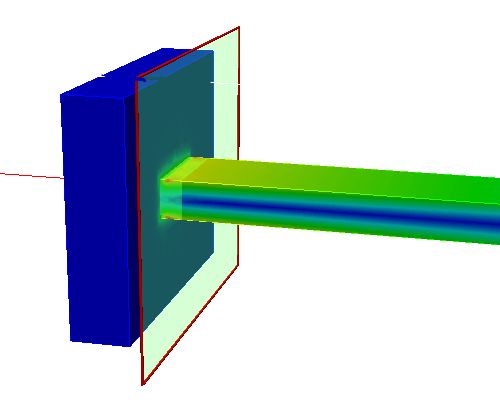
特異点を避けて応力評価するとほぼ理論値と一致
理論値は150MPaでした。測定面におけるミーゼス応力は148.1MPa、主応力は150.6MPaと表示されており、理論値の150MPaとほぼおなじ値になっています。
ミーゼス応力(148.1MPa)
主応力(150.6MPa)

特異点を避けて応力を測定すれば、ほぼ理論値と同等の値になることが確認できました。特異点による応力集中の有無は人間が判別しなければなりません。将来はコンピューターが自動判定してくれるようになるかもしれませんが、現在は応力評価を人間の手で行うことが求められます。
角度が変化している箇所、拘束面の近傍では、特異点による応力集中が起きやすいので、CAEの表示結果を鵜呑みにせずに測定点を検討しましょう。
また、全ての角をフィレットにすれば角度変化は少なくなりますが、細かすぎる形状ではメッシュ作成が難しくなる場合があります。実際に機械加工できないようなRにすると解析に失敗することもあるので、特異点発生を避けるためだけのモデル修正はしない方が無難です。
特異点がある場合の応力評価
CAEを活用すれば、人間には処理できない複雑な形状でも解析することができますが、特異点という思わぬ落とし穴が存在しています。応力の特異点が存在する場合、最大応力を正しく評価するためのポイントは次の4つです。
- 近似図形の理論値が計算できるのであれば、参考にする
- メッシュの角度が変化している箇所では特異点の存在を疑う
- 拘束面の近傍では特異点の存在を疑う
- 解析条件を変えて複数回の解析を行い、応力の特異点かどうか判断する
- 応力の特異点があれば、応力集中箇所を避けて最大応力を求める
上記の1~4までは、全て特異点かどうかを判断するための方法で、特異点になりそうな箇所に予め見当をつけることができます。特異点であることがわかれば、応力を過剰評価してしまう可能性を少なくすることができます。
逆説的ですが、特異点が存在すると最大応力は高めに算出されるため、結果として設計が安全サイド寄りになります。そのため、設計に余裕がある場合は、正確な応力評価にこだわらず、特異点の最大応力を採用することで、設計条件以上の荷重条件がかかっても破壊されない安全な構造にすることができます。